Latitude, usually denoted symbolically by the Greek letter phi, , gives the location of a place on Earth north or south of the equator. Lines of Latitude are the horizontal lines shown running east-to-west on maps. Technically, Latitude is an angular measurement in degrees (marked with °) ranging from 0° at the Equator (low latitude) to 90° at the poles (90° N for the North Pole or 90° S for the South Pole; high latitude). The complementary angle of a latitude is called the colatitude.

Circles of latitude
Besides the equator, four other lines of latitude are named because of the role they play in the geometrical relationship with the Earth and the Sun:
Only at latitudes between the Tropics is it possible for the sun to be at the zenith. Only north of the Arctic Circle or south of the Antarctic Circle is the midnight sun possible.
The reason that these lines have the values that they do lies in the axial tilt of the Earth with respect to the sun, which is 23° 26′ 21.41″.
Note that the Arctic Circle and Tropic of Cancer and the Antarctic Circle and Tropic of Capricorn are colatitudes since the sum of their angles is 90°.

Arctic Circle — 66° 33′ 39″ N
Tropic of Cancer — 23° 26′ 21″ N
Tropic of Capricorn — 23° 26′ 21″ S
Antarctic Circle — 66° 33′ 39″ S Important named circles of latitude
As Earth is not a smooth sphere, but slightly oblate, a degree of latitude varies in length from about 111.3195 km at the equator to 110.9462 km at the poles. A degree of arc at a latitude not only varies with latitude, but also with the direction being faced. To simplify calculations where elliptical consideration is not important, the nautical mile was created, equaling exactly 111.12 km per degree of arc or, sub-dividing into minutes, 1852 metres per minute of arc. One minute of latitude can be further divided into 60 seconds. A latitude is thus specified as 13°19'43″ N (for greater precision, a decimal fraction can be added to the seconds). An alternative representation uses only degrees and minutes, where the seconds are expressed as a decimal fraction of minutes, thus the above example is expressed as 13°19.717' N. Degrees can also be expressed singularly, with both the minutes and seconds incorporated as a decimal number and rounded as desired (decimal degree notation): 13.32861° N. Sometimes, the north/south suffix is replaced by a negative sign for south (−90° for the South Pole).

Effect of latitude
Because the Earth is slightly flattened by its rotation, cartographers refer to a variety of auxiliary latitudes to precisely adapt spherical projections according to their purpose. More generally, for other planets such as Mars, geographic and geocentric latitude are called "planetographic" and "planetocentric" latitude, respectively. Most maps of Mars since 2002 use planetocentric coordinates.

Types of latitude
The expressions following assume elliptical polar sections with the angular eccentricity, (which equals , where and are the equatorial and polar radii), and that all sections parallel to the equatorial plane are circular. Geographic latitude (with longitude) then provides a Gauss map.

In common usage, "latitude" refers to geodetic or geographic latitude and is the angle between the equatorial plane and a line that is normal to the reference spheroid, which approximates the shape of the Earth to account for flattening of the poles and bulging of the equator. Common "latitude"

Reduced or parametric latitude, , is the latitude of the same radius on the sphere with the same equator. Reduced latitude

Authalic latitude, , gives an area-preserving transform to the sphere. Authalic latitude

 

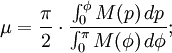
Rectifying latitude, , is the surface distance from the equator, scaled so the pole is 90°. Unfortunately, it involves elliptic integration: Rectifying latitude

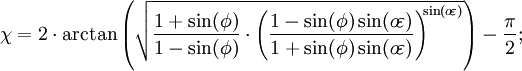
Conformal latitude, , gives an angle-preserving (conformal) transform to the sphere. Conformal latitude

The geocentric latitude,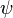 , is the angle between the equatorial plane and a line from the center of the Earth. Geocentric latitude
The following plot shows the differences between the types of latitude. The data used is found in the table following the plot. Please note that the values in the table are in minutes, not degrees, and the plot reflects this as well. Also note that the conformal symbols are hidden behind the geocentric due to being very close in value.

Approximate difference from geographic latitude ("Lat")
Lat	Reduced	Authalic	Rectifying	Conformal	Geocentric
0°	0.00′	0.00′	0.00′	0.00′	0.00′
5°	1.01′	1.35′	1.52′	2.02′	2.02′
10°	1.99′	2.66′	2.99′	3.98′	3.98′
15°	2.91′	3.89′	4.37′	5.82′	5.82′
20°	3.75′	5.00′	5.62′	7.48′	7.48′
25°	4.47′	5.96′	6.70′	8.92′	8.92′
30°	5.05′	6.73′	7.57′	10.09′	10.09′
35°	5.48′	7.31′	8.22′	10.95′	10.96′
40°	5.75′	7.66′	8.62′	11.48′	11.49′
45°	5.84′	7.78′	8.76′	11.67′	11.67′
50°	5.75′	7.67′	8.63′	11.50′	11.50′
55°	5.49′	7.32′	8.23′	10.97′	10.98′
60°	5.06′	6.75′	7.59′	10.12′	10.13′
65°	4.48′	5.97′	6.72′	8.95′	8.96′
70°	3.76′	5.01′	5.64′	7.52′	7.52′
75°	2.92′	3.90′	4.39′	5.85′	5.85′
80°	2.00′	2.67′	3.00′	4.00′	4.01′
85°	1.02′	1.35′	1.52′	2.03′	2.03′
90°	0.00′	0.00′	0.00′	0.00′	0.00′

Comparison of latitudes
A more obscure measure of latitude is the astronomical latitude, which is the angle between the equatorial plane and the normal to the geoid (ie a plumb line). It originated as the angle between horizon and pole star.
Astronomical latitude is not to be confused with declination, the coordinate astronomers use to describe the locations of stars north/south of the celestial equator (see equatorial coordinates), nor with ecliptic latitude, the coordinate that astronomers use to describe the locations of stars north/south of the ecliptic (see ecliptic coordinates).

Astronomical latitude
Continents move over time, due to continental drift, taking whatever fossils and other features of interest they may have with them. Particularly when discussing fossils, it's often more useful to know where the fossil was when it was laid down, than where it is when it was dug up: this is called the palæolatitude of the fossil. The Palæolatitude can be constrained by palæomagnetic data. If tiny magnetisable grains are present when the rock is being formed, these will align themselves with the Earth's magnetic field like compass needles. A magnetometer can deduce the orientation of these grains by subjecting a sample to a magnetic field, and the declination of the grains can be used to infer the latitude of deposition.

Palæolatitude

John P. Snyder Map Projections: a working manual excerpts See also